前回の「感染症のシミュレーション」ではセルオートマトンによる計算を行いました。
今回は、SIRモデルと呼ばれる感染症の数理モデルを用いて計算してみます。
尚、今回も新型コロナウイルス感染症のデータを用いていますが、新型コロナウイルス感染症のシミュレーションというわけではありません。実際のシミュレーションには、より厳密なモデルと多くの観測データから得られる適切なパラメータが必要です。
■SIRモデルとは
例えば以下のような文献があります。
https://www.ms.u-tokyo.ac.jp/~inaba/inaba_science_2008.pdf
ケルマックとマッケンドリックにより提案された感染症流行モデルです。
S(t)はsusceptiblesを意味し、時刻tにおける感染する可能性のある人口、すなわち未感染の人口です。
I(t)はinfectivesを意味し、時刻tにおいて感染していて、感染させる能力のある人口です。
R(t)はrecoverdを意味し、時刻tにおける主に回復して免疫保持者となった人々です。死亡者や隔離された人々も含みます。よく手洗いをして感染しない人々もこれに含めてよいでしょう。
さらに感染率をβ(ベータ)とします。感染した人1人が単位時間当たりにまだ感染していない人1人に感染させる確率です。
また、隔離率をγ(ガンマ)とします。感染した人が単位時間あたりに治癒する確率です。
さて、
時刻tにおける未感染者数は、新規感染者数であるβS(t)I(t)だけ減ります。
時刻tにおける感染者数は、新規感染者数であるβS(t)I(t)だけ増えて、新規治癒者数であるγI(t)だけ減ります。
時刻tにおける治癒者数は、新規治癒者数であるγI(t)だけ増えます。
これらを微分方程式というもので表すと
dS(t)/dt = −βS(t)I(t)
dI(t)/dt = βS(t)I(t) − γI(t)
dR(t)/dt = γI(t)
となります。
これは1階連立常微分方程式と呼ばれるものなので当プログラミング教室の「データサイエンスとAIの初歩」コースでも用いているPythonで簡単に解けます。
尚、都市の人口Nは1400万人、
回復日数Dは2週間、すなわち14日、
基本再生産数R0は1.5, 2.0, 2.5の3種類として計算しました。
基本再生産数は1人の感染者が何人の人に感染させるかを表す重要なパラメータです。
■Pythonのプログラムは以下のようになります。
# SIRモデル
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# 1階連立常微分方程式
def func(var, t, beta, gamma):
dSdt = -beta*var[0]*var[1]
dIdt = beta*var[0]*var[1] - gamma*var[1]
dRdt = gamma*var[1]
return [dSdt, dIdt, dRdt]
# グラフ
def plot2d(t_list, y_list, t_label, y_label):
plt.xlabel(t_label)
plt.ylabel(y_label)
plt.grid()
plt.plot(t_list, y_list)
# パラメータ設定
dt = 0.1 # 時間間隔
t_list = np.arange(0, 1000, dt)
D = 14 # 回復日数
gamma = 1/D # 回復率
R0 = 2.5 # 基本再生産数
N = 1.4e7 # 都市の人口
beta = R0*gamma/N # 感染確率
#print(lamb, gamma)
# 初期値設定
I1 = 1
R1 = 0
#R1 = N * 0.3
S1 = N-I1-R1
var_init = [S1, I1, R1]
# 微分方程式を解く
var_list = odeint(func, var_init, t_list, args=(beta, gamma))
#print(var_list)
# 結果の処理
infection = var_list[:, 1]
max_infection = int(np.max(infection))
max_infection_index = np.argmax(infection)
print('感染者数の最大値', max_infection)
print('最大値をとる日数', int(t_list[max_infection_index]))
print('最終的な人口に対する感染経験者の割合', var_list[:, 2][t_list.size-1]/N*100)
# 可視化
plot2d(t_list, var_list[:, 0], "days", "y(t)")
plot2d(t_list, var_list[:, 1], "days", "y(t)")
plot2d(t_list, var_list[:, 2], "days", "y(t)")
plt.legend(['Susceptibles','Infectives', 'Recovered'])
plt.show()
# グラフの保存
#plt.savefig('infection3.png')
■計算結果
下のグラフで横軸は日数を表します。
青線は未感染者数、オレンジ色の線は感染させる能力のある人の数、緑色の線は回復して免疫をつけた人の数です。
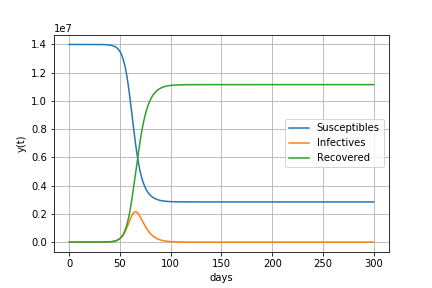
基本再生産数R0が1.5の場合
すなわち1人の感染者が1.5人に感染させる場合
感染が始まってから427日後に88万人の感染者がいます。
最終的に58%の人が感染します。
感染者数の最大値 882326 最大値をとる日数 427 最終的な人口に対する感染経験者の割合 58%
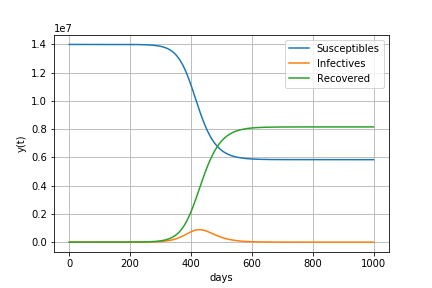
基本再生産数R0が2.0の場合
すなわち1人の感染者が2.0人に感染させる場合
感染が始まってから228日後に214万人の感染者がいます。
最終的に80%の人が感染します。
感染者数の最大値 2147966 最大値をとる日数 228 最終的な人口に対する感染経験者の割合 80%
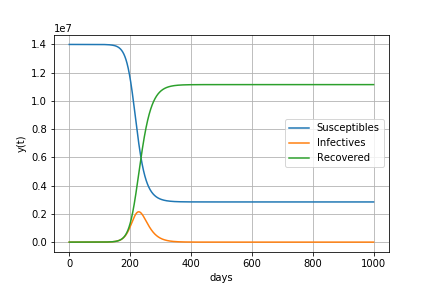
基本再生産数R0が2.5の場合
すなわち1人の感染者が2.5人に感染させる場合
感染が始まってから157日後に327万人の感染者がいます。
最終的に89%の人が感染します。
感染者数の最大値 3268772 最大値をとる日数 157 最終的な人口に対する感染経験者の割合 89%
基本再生産数R0をできるだけ1に近づけること、すなわち、自分が感染したとしても他人に移さないということが非常に大事です。
尚、自分が手洗いなどを頻繁に行い感染しないということも、R(t)の初期値を高めることに寄与するため感染拡大防止に有効です。
■補足
政府の新型コロナウイルス感染症対策専門家会議で西浦教授から示されたパラメータを用いて再計算したものを下に示します。
報告されている結果とほぼ同じ結果が得られました。
何も対策を講じない最悪の場合は、このようになることもあり得るということです。
https://www.m3.com/open/iryoIshin/article/738238/
https://www.kantei.go.jp/jp/singi/novel_coronavirus/senmonkakaigi/sidai_r020302.pdf
回復日数Dは4日、
基本再生産数R0は低位の1.4, 中位の1.7, 高位の2.0の3種類として計算しました。
基本再生産数R0が1.4の場合
すなわち1人の感染者が1.4人に感染させる場合
感染が始まってから149日後に64万人の感染者がいます。
感染者数が減少に転じるときの(感染者+感染経験者)の割合は29%
最終的に51%の人が感染します。
感染者数の最大値 635278 最大値をとる日数 149 感染者が減少に転じるときの(感染者+感染経験者)の割合 29.0 最終的な人口に対する感染経験者の割合 51.0
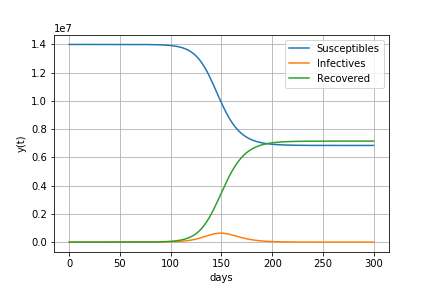
基本再生産数R0が1.7の場合
すなわち1人の感染者が1.7人に感染させる場合
感染が始まってから90日後に139万人の感染者がいます。
感染者数が減少に転じるときの(感染者+感染経験者)の割合は41%
最終的に69%の人が感染します。
感染者数の最大値 1394821 最大値をとる日数 90 感染者が減少に転じるときの(感染者+感染経験者)の割合 41.0 最終的な人口に対する感染経験者の割合 69.0
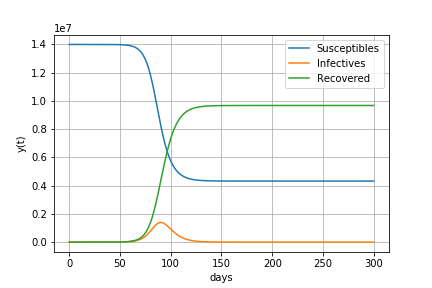
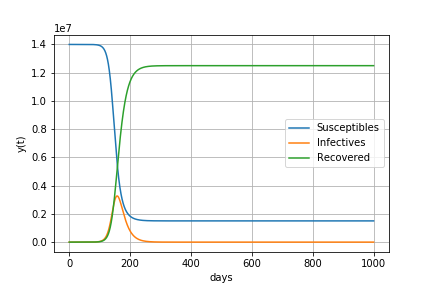
基本再生産数R0が2.0の場合
すなわち1人の感染者が2.0人に感染させる場合
感染が始まってから65日後に215万人の感染者がいます。
感染者数が減少に転じるときの(感染者+感染経験者)の割合は50%
最終的に80%の人が感染します。
感染者数の最大値 2147953 最大値をとる日数 65 感染者が減少に転じるときの(感染者+感染経験者)の割合 50.0 最終的な人口に対する感染経験者の割合 80.0