例えば三角関数を使って波を描き、これを時間とともに移動するアニメーションを作成したりしていますが、移動する仕組みでひっかかる生徒さんが多いのが現状です。
まず、三角関数の代わりに直線のグラフを使ってグラフを平行移動させるにはどうすればいいのかを考えてみましょう。
直線の式として
y = x
を想定します。
これをグラフにすると傾き1の右肩上がりの直線になります。
それでは
y = x-1
のグラフはどのようになるでしょうか?
直線の傾きは1のままです。
x=1とするとy=0になるので、右に1だけずれた直線になります。
y = x-2
のグラフはどのようになるでしょうか?
x=2とするとy=0になるので、右に2だけずれた直線になることがわかります。
それでは一般に
y = x-a
のグラフはどのようになるでしょうか?
直線の傾きは1のままであり、x=aでy=0になるので、右にaだけずれた直線になるわけです。
実際にPythonでグラフを描いてみましょう。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-3, 3, 0.1)
y0 = x
y1 = x-1
y2 = x-2
plt.plot(x, y0, label='x')
plt.plot(x, y1, label='x-1')
plt.plot(x, y2, label='x-2')
plt.xlabel('x')
plt.ylabel('y')
plt.title('y=f(x-a)')
plt.grid()
plt.legend()
plt.savefig('y=x-a.png')
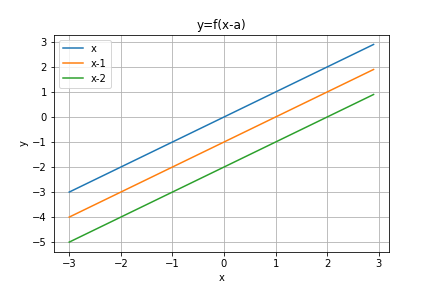
上記のことは一般に言えます。
yがxの関数であるとき、
y = f(x)
と書きますが、
y = f(x-a)のグラフはy = f(x)のグラフを右にaだけ移動したグラフになります。
サイン関数でも同様です。
y = sin(x-1)のグラフはy = sin(x)のグラフを右に1だけ移動したグラフです。
y = sin(x-2)のグラフはy = sin(x)のグラフを右に2だけ移動したグラフです。
y = sin(x-a)のグラフはy = sin(x)のグラフを右にaだけ移動したグラフです。
実際にグラフを描いてみましょう。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-3, 3, 0.1)
y0 = np.sin(x)
y1 = np.sin(x-1)
y2 = np.sin(x-2)
plt.plot(x, y0, label='sin(x)')
plt.plot(x, y1, label='sin(x-1)')
plt.plot(x, y2, label='sin(x-2)')
plt.xlabel('x')
plt.ylabel('y')
plt.title('y=f(x-a)')
plt.grid()
plt.legend()
plt.savefig('y=sin(x-a).png')
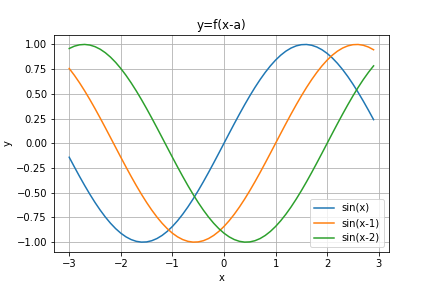
さて、以上のことから、グラフを時間とともに移動するには
y = f(x-t)
の式において、
t=t1のときのグラフを描き、
t=t2のときのグラフを描き、
t=t3のときのグラフを描き、
その後もtの値を増やしながらグラフを描けば良いことになります。
サイン関数の場合は以下のようになります。
%matplotlib nbagg
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
fig = plt.figure(figsize=(4, 3))
x = np.arange(0, 10, 0.1)
images = []
for t in np.arange(0, 50, 0.1):
y = np.sin(x - t)
image = plt.plot(x, y, 'r')
images.append(image)
ani = animation.ArtistAnimation(fig, images)
#ani.save('sin.gif', writer='pillow')
ani.save('sin.mp4', writer='ffmpeg', fps=30)

