生徒に教えてもらった1989年の東大入試問題です。
3個の赤玉とn個の白玉を無作為に環状に並べるものとする。このとき白玉が連続してk+1個以上並んだ箇所が現れない確率を求めよ。ただしn/3<=k<n/2とする。
有名な問題のようで、ネットで検索するといくつも解答例が出て来ます。
どれもが、赤玉にはさまれる白玉の個数をa, b, cとして延々と解いています。
しかし、東大入試問題にはエレガントな解法がある場合がよくあります。
ラテラルシンキングで逆転の発想をしてみましょう。
実は、赤玉にはさまれる白玉の個数を全てk個としてしまえば簡単です。ただし、k個には空席も含まれるとするのです。
以下に具体的に説明しましょう。
赤玉をR1, R2, R3とし、R1を固定して考えます。
まず、全体の場合の数は白玉n個+赤玉2個の(n+2)個から赤玉2個を選ぶ組み合わせの数なので、
(n+2)C2通り。
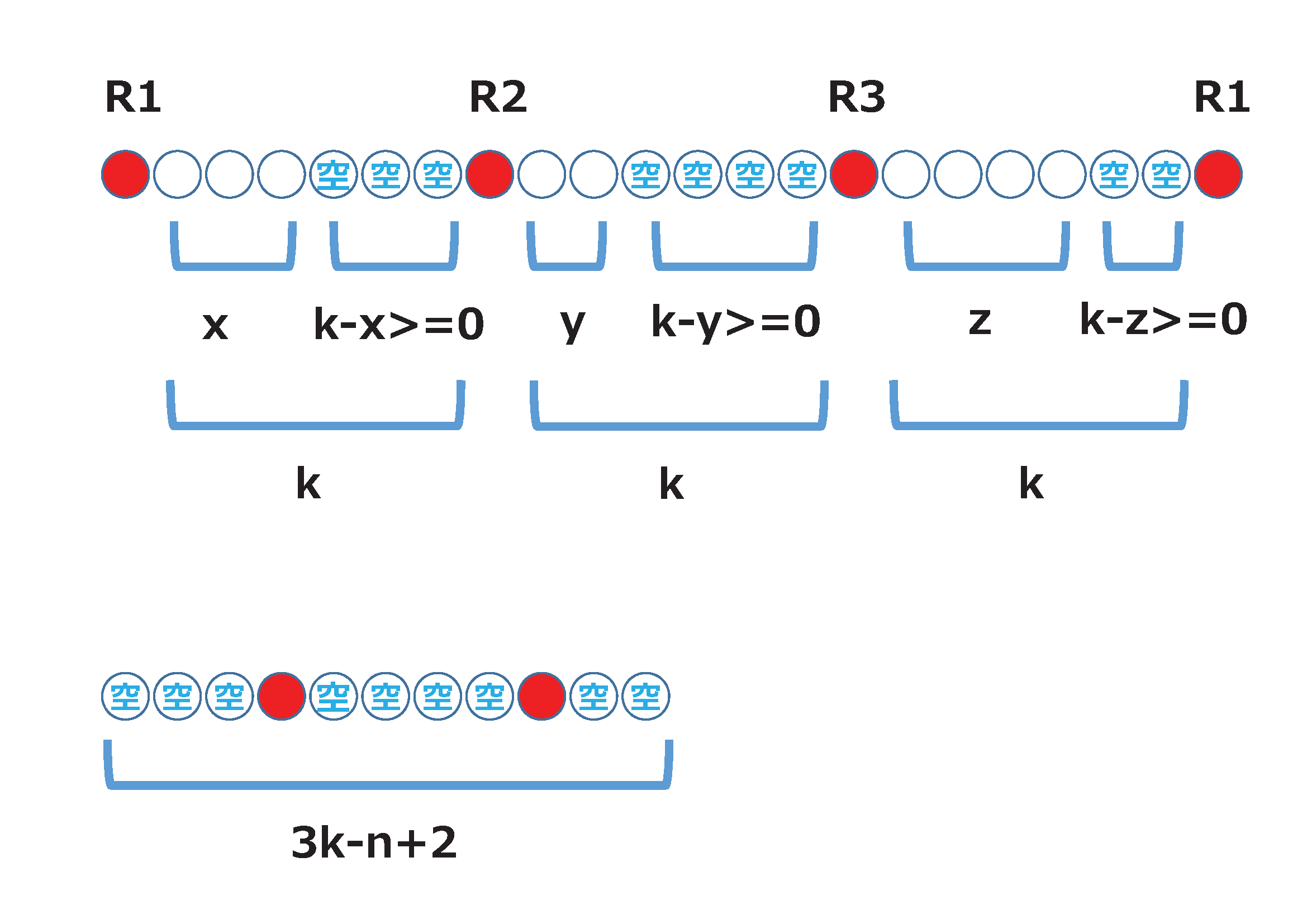
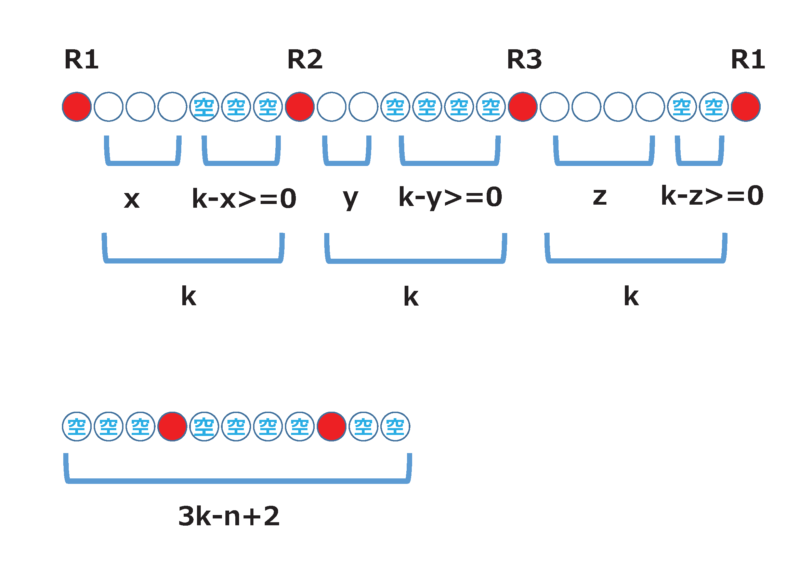
次に下図(上の方)のように空席を含めて考えます。空席の数はk-x>=0, k-y>=0, k-z>=0です。
空席は全部で3k-(x+y+z)=3k-n個あります。
下図(下の方)のように空席と赤玉2個の合計3k-n+2個から赤玉2個を選ぶ組み合わせは
(3k-n+2)C2通り。
よって求める確率をpとすると
p=(3k-n+2)C2 / (n+2)C2=(3k-n+2)(3k-n+1)/((n+2)(n+1))
この方法なら3分もあれば解けるでしょう。
せっかくなので、具体的に確率を計算してみましょう。
n=10000として、kを所定の範囲で変化させ、そのときの確率pを計算します。
Pythonのプログラムは以下のようにすれば良いでしょう。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
n=10000
k1=int(n/3)+1
k2=int(n/2)
print(k1, k2)
k = np.arange(k1, k2)
p = (3*k-n+2)*(3*k-n+1)/(n+2)/(n+1)
plt.plot(k, p)
plt.xlabel('k')
plt.ylabel('p')
plt.title('p = (3*k-n+2)*(3*k-n+1)/(n+2)/(n+1)')
plt.grid()
plt.savefig('p=f(k).png')
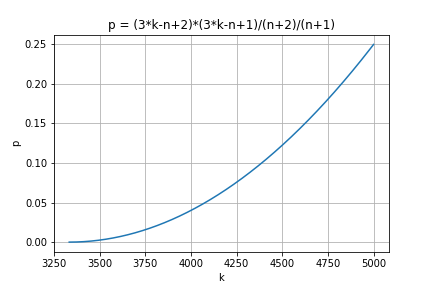
kを横軸に、pを縦軸にとったグラフが以下のグラフです。
nが十分大きいとき、kの最大値においてpは0.25に近づいていくことがわかります。