2進数の加算回路を全員が学ぶ時代
高校の情報Iの教科書を見ると、どの教科書にも2進数の加算回路について説明しています。情報Iは必修科目で1年次に学ぶので、これからは全員が学ぶことになります。共通テストに出題されることもあるでしょう。
実際にProcessingとPythonのそれぞれで加算回路を作ってみましょう。
基本回路の説明
■基本回路
CPU内部では複数の論理回路を組み合わせることで複雑な演算を行っています。論理値の真(true)を1、偽(false)を0として扱います。
論理回路の基本としてはAND回路、OR回路、NOT回路があり、この3つの組み合わせで様々な論理回路を構成できます。
AND回路は2つの入力と1つの出力を持ちます。2つの入力がともに1の時だけ、出力が1になります。
OR回路は2つの入力と1つの出力を持ちます。入力のいずれか一方が1であれば、出力が1になります。
NOT回路は1つの入力と1つの出力を持ちます。入力した信号を反転した値を出力します。
■半加算回路
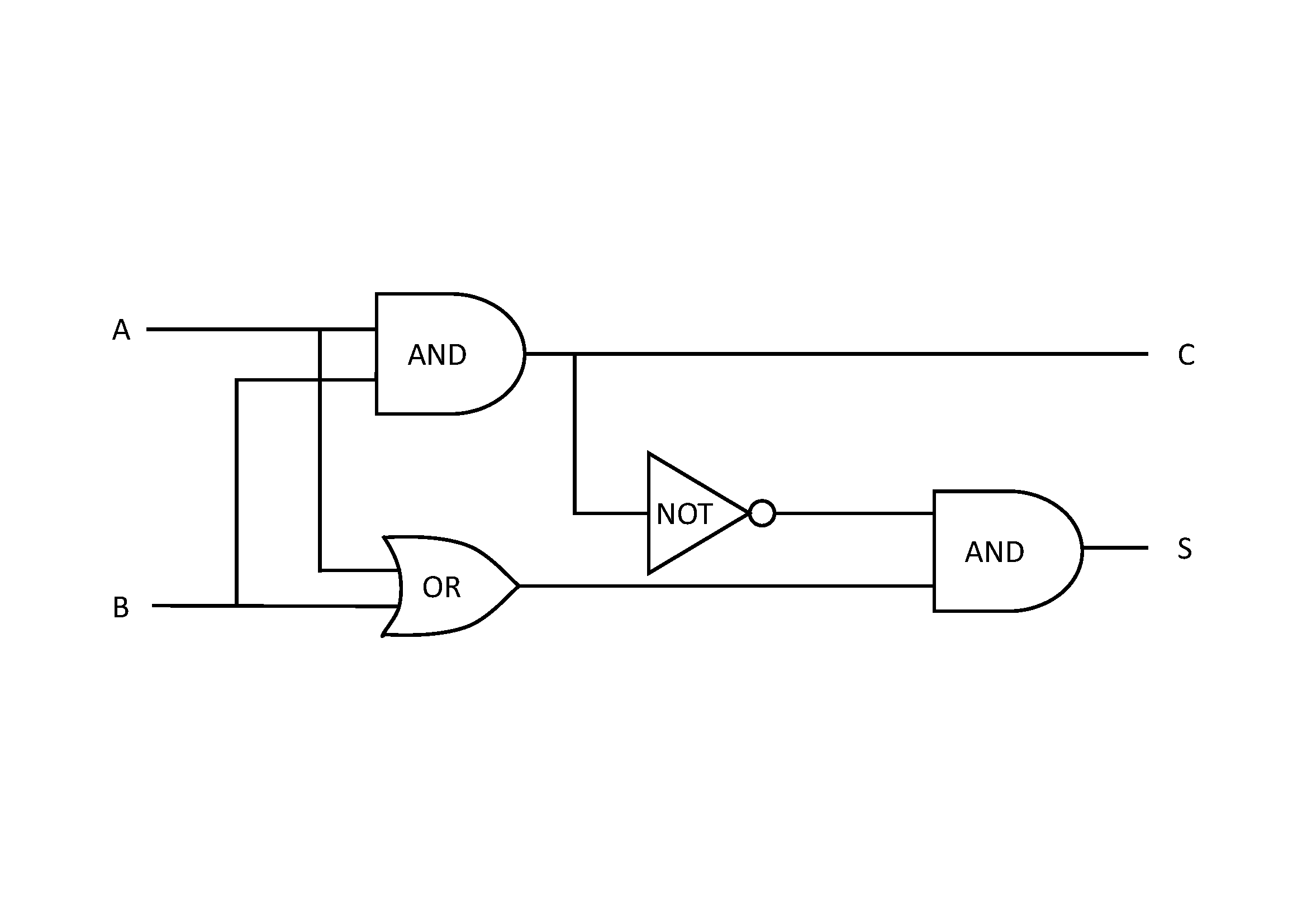
以下の図のようなAND回路、OR回路、NOT回路を組み合わせた回路を半加算回路と呼びます。
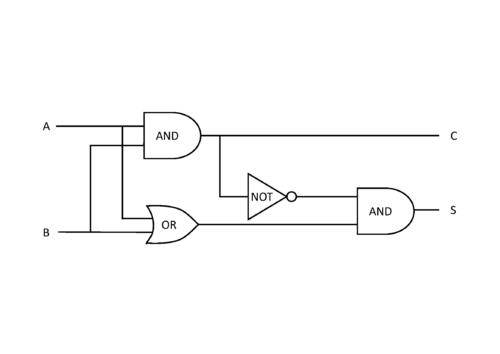
入力はA、Bで出力は桁上がりC(Carry)と和S(Sum)です。
すなわち、2進数の1桁の加算ができる論理回路です。
例えば、A=1, B=1のとき、C=1, S=0となります。
■全加算回路
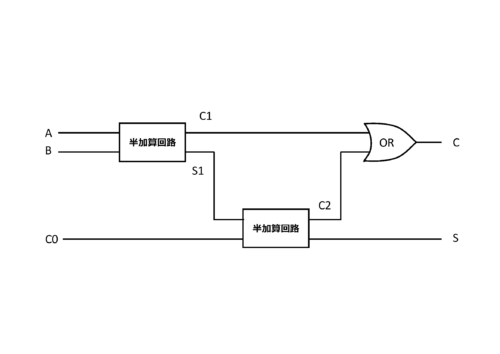
半加算回路では1桁の計算しかできませんでしたが、下図のように半加算回路を組み合わせることで、下からの桁上がりを考慮した加算器ができます。これを全加算回路と呼びます。
この全加算回路をさらに組み合わせれば、任意の桁数の加算回路が実現できます。
プログラムで加算回路を作ってみる
■Processingの場合
以下のようなプログラムで半加算回路と全加算回路を作ることができます。入力と出力を図と照らし合わせながら確認すると良いでしょう。2進数3桁の計算を行なっています。
入力 x 0 0 1
入力 y 1 1 1
の場合
桁上がり c 1 1 1
和 s 0 0 0
が確認できます。
桁が上がって1000になりますが、3桁の計算にしているのでsは000です。
boolean carry, sum;
void setup() {
boolean[] x = new boolean[3];
boolean[] y = new boolean[3];
boolean[] c = new boolean[3];
boolean[] s = new boolean[3];
x[0] = true;
x[1] = false;
x[2] = false;
y[0] = true;
y[1] = true;
y[2] = true;
halfAdder(x[0], y[0]);
c[0] = carry;
s[0] = sum;
fullAdder(x[1], y[1], c[0]);
c[1] = carry;
s[1] = sum;
fullAdder(x[2], y[2], c[1]);
c[2] = carry;
s[2] = sum;
println("x", int(x[2]), int(x[1]), int(x[0]));
println("y", int(y[2]), int(y[1]), int(y[0]));
println("c", int(c[2]), int(c[1]), int(c[0]));
println("s", int(s[2]), int(s[1]), int(s[0]));
}
boolean AND(boolean a, boolean b) {
return a && b;
}
boolean OR(boolean a, boolean b) {
return a || b;
}
boolean NOT(boolean a) {
a = (a == false)? (a = true):(a = false);
return a;
}
void halfAdder(boolean a, boolean b) {
boolean or1, and1, not1, and2;
or1 = OR(a, b);
and1 = AND(a, b);
not1 = NOT(and1);
and2 = AND(or1, not1);
carry = and1;
sum = and2;
}
void fullAdder(boolean a, boolean b, boolean c0) {
boolean halfAdder_c1, halfAdder_s1, halfAdder_c2, halfAdder_s2, or;
halfAdder(a, b);
halfAdder_c1 = carry;
halfAdder_s1 = sum;
halfAdder(halfAdder_s1, c0);
halfAdder_c2 = carry;
halfAdder_s2 = sum;
or = OR(halfAdder_c1, halfAdder_c2);
carry = or;
sum = halfAdder_s2;
}
■Pythonの場合
この場合も以下のようなプログラムで半加算回路と全加算回路を作ることができます。入力と出力を図と照らし合わせながら確認すると良いでしょう。2進数3桁の計算を行なっています。
import numpy as np
x = [True, False, False]
y = [True, True, True]
c = []
s = []
def AND(a, b):
return a and b
def OR(a, b):
return a or b
def NOT(a):
return not a
def half_adder(a, b):
or1 = OR(a, b)
and1 = AND(a, b)
not1 = NOT(and1)
and2 = AND(or1, not1)
return and1, and2
def full_adder(a, b, c0):
c_and_s = half_adder(a, b)
halfAdder_c1 = c_and_s[0]
halfAdder_s1 = c_and_s[1];
c_and_s = half_adder(halfAdder_s1, c0)
halfAdder_c2 = c_and_s[0]
halfAdder_s2 = c_and_s[1];
or_ = OR(halfAdder_c1, halfAdder_c2)
return or_, halfAdder_s2
c_and_s = half_adder(x[0], y[0])
c.append(c_and_s[0])
s.append (c_and_s[1])
c_and_s = full_adder(x[1], y[1], c[0])
c.append(c_and_s[0])
s.append (c_and_s[1])
c_and_s = full_adder(x[2], y[2], c[1])
c.append(c_and_s[0])
s.append (c_and_s[1])
print("x", [int(i) for i in list(reversed(x))])
print("y", [int(i) for i in list(reversed(y))])
print("c", [int(i) for i in list(reversed(c))])
print("s", [int(i) for i in list(reversed(s))])
以下の出力が得られます。
x [0, 0, 1] y [1, 1, 1] c [1, 1, 1] s [0, 0, 0]
まとめ
教科書に書いてあることも、プログラムを使って実際にやってみることでより理解が深まります。