■報道によれば人との接触を80%削減すると新型コロナウイルスの新規感染者数を短期間で大幅に削減できるとのことです。
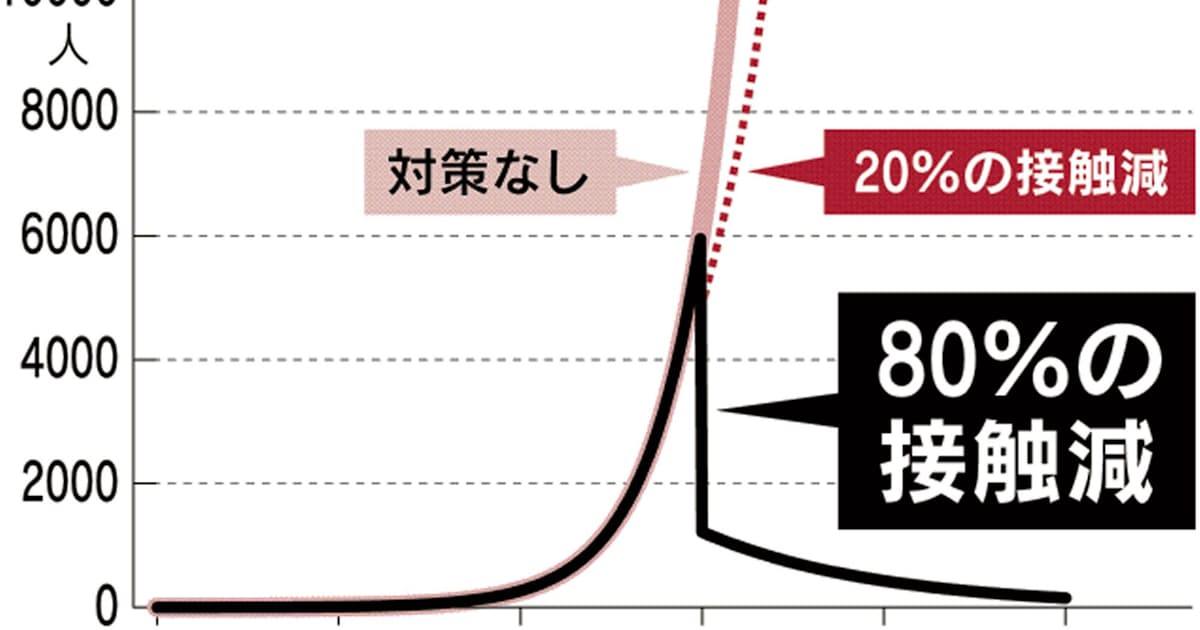
ここでも、クリティカルシンキングが大事です。
今回は人との接触の削減効果を実際にシミュレーションしてみましょう。
■結論として
1.報告されているものとほぼ同じ結果(80%削減が効果的など)が得られました。
2.ただし、使用するパラメータ(基本再生産数など)を変えれば結果も変化するので注意が必要です。どのパラメータを使えば良いかは現時点でよくわかってないと思います。
3.人との接触をある期間だけ削減しても、削減期間が終わってまた再度接触するようになれば、再び新規感染者数は増大の一途をたどります。単純に元と同じ環境に戻るだけではダメだということです。何らかの対策が必要です。
■シミュレーション方法は「感染症のシミュレーション2」に説明したのと同じSIR感染モデルを使います。
ここで、ある時間に基本再生産数(1人の感染者が何人にうつすか)を人との接触を減らした効果として急に減らしてみます。実際に効果が現れるのにはある一定の時間が必要ですが、ここでは単純化したモデルにしました。
例えば、接触を80%削減した場合は、基本再生産数を2.5としてこれを0.2倍するだけです。接触削減率として0, 20, 40, 50, 60, 70, 80, 90%の場合について計算しました。
グラフの横軸は日数で、縦軸は1日の新規感染者です。全体像がわかりやすいように縦軸を対数スケールにしたものも示します。
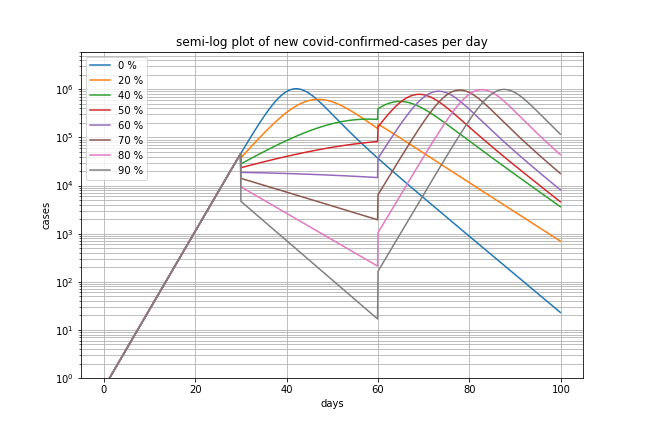
■シミュレーション結果1
基本再生産数を2.5として接触削減率を0, 20, 40, 50, 60, 70, 80, 90%とした場合
この場合、理論上は削減率60%で1人が1人にうつすようになります。削減率がこれより少ないと新規感染者数は増大していきます。70%で減少効果がみられますが、80%ではより短期間で減少することがわかります。
同じものを片対数でプロットしたのが次のグラフです。
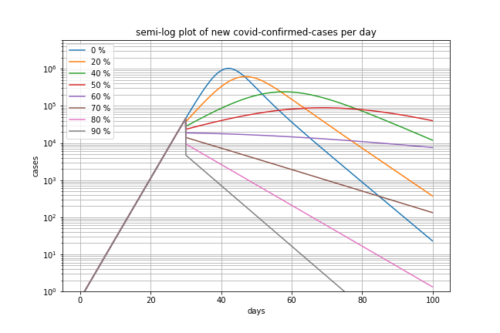
より、全体像がわかります。
直線的に減少しているのは、指数関数的に減少していることを意味しています。
■シミュレーション結果2
基本再生産数を1.56として接触削減率を0, 20, 40, 50, 60, 70, 80, 90%とした場合
前回、東京都の場合は、基本再生産数を1.56とすると実際のデータとよく合っていたのでこの数値を用いて計算してみました。
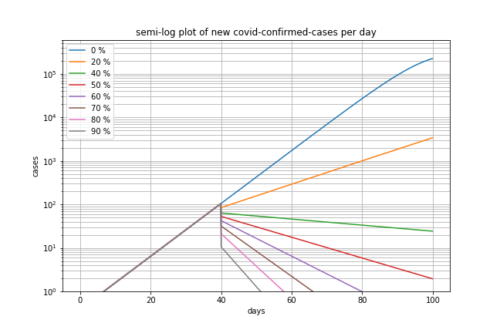
例えば、削減率50%程度でもそこそこ効果はあることがわかります。
このようにシミュレーションに使うパラメータの値によって、結果は異なるため注意が必要です。今後も実際の観測データからより適切なパラメータを求める必要があります。
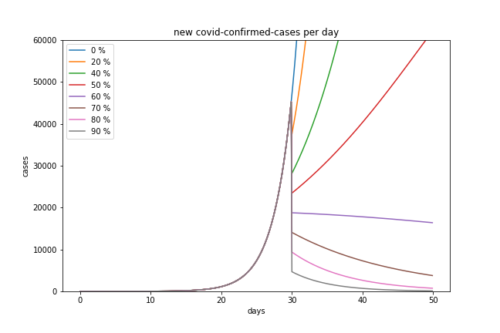
■シミュレーション結果3
基本再生産数を2.5として接触削減率を0, 20, 40, 50, 60, 70, 80, 90%とし、さらに削減してから30日後に接触削減を解除した場合
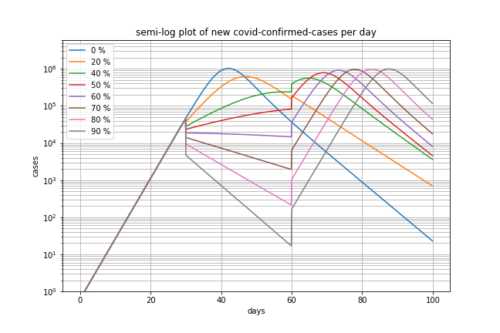
例えばピンクの線で示したように接触削減率が80%であっても接触削減の解除後は再び新規感染者数は指数関数的に増大していきます。感染ピークを遅らせているだけです。よく考えてみれば当たり前かもしれません。
従って、接触削減の解除後にこうならないようにする何らかの方策が必要であることがわかります。