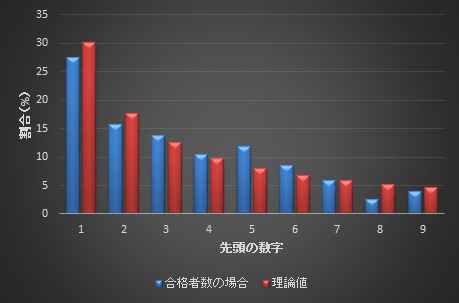
数字のたくさん載った資料を持ってきて、先頭の数字に着目します。
例えば先頭の数が1である割合は、1/9のように思われますが、実際には30%近いことが多いです。
逆に先頭の数が9である割合は数%程度です。
一般に先頭の数字がnとなる確率は
$\begin{align}
p_n &= \log (n+1) – \log n
\end{align}$
これをベンフォードの法則といいます。
数字のデータが2のべき乗の場合についてベンフォードの法則が何故成り立つかを直感的に確かめてみましょう。
■先頭の数字が1となる場合
以下の特殊ケースについて考える。
$2^1, 2^2, 2^3, \cdots , 2^{100}$
について、先頭の数字が1となる場合を求める。
先頭の数字が1となる条件は
$1 \times 10^m \leq 2^k < 2 \times 10^m$
常用対数をとると
$m \leq k \log 2 < m + \log 2$
kの満たすべき条件は
$\begin{align}
\frac{m}{\log 2} \leq k < \frac{m + \log 2}{\log 2}
\end{align}$
$k$が入る区間の幅を$x_1$とすると
$\begin{align}
x_1 &= \frac{m + \log 2}{\log 2} – \frac{m}{\log 2}\\
&= 1
\end{align}$
■先頭の数字が2となる場合
同様にして先頭の数字が2となる条件は
$2 \times 10^m \leq 2^k < 3 \times 10^m$
常用対数をとると
$m + \log 2 \leq k \log 2 < m + \log 3$
kの満たすべき条件は
$\begin{align}
\frac{m + \log 2}{\log 2} \leq k < \frac{m + \log 3}{\log 2}
\end{align}$
$k$が入る区間の幅を$x_2$とすると
$\begin{align}
x_2 &= \frac{m + \log 3}{\log 2} – \frac{m + \log 2}{\log 2}\\
&= \frac{\log 3 – \log 2}{\log 2}
\end{align}$
■先頭の数字が3となる場合
同様にして先頭の数字が3となる条件は
$3 \times 10^m \leq 2^k < 4 \times 10^m$
常用対数をとると
$m + \log 3 \leq k \log 2 < m + \log 4$
kの満たすべき条件は
$\begin{align}
\frac{m + \log 3}{\log 2} \leq k < \frac{m + \log 4}{\log 2}
\end{align}$
$k$が入る区間の幅を$x_3$とすると
$\begin{align}
x_3 &= \frac{m + \log 4}{\log 2} – \frac{m + \log 3}{\log 2}\\
&= \frac{\log 4 – \log 3}{\log 2}
\end{align}$
■先頭の数字がnとなる場合
一般に先頭の数字が$n$($= 1, 2, 3, \cdots , 9$)となる条件は
$n \times 10^m \leq 2^k < (n+1) \times 10^m$
常用対数をとると
$m + \log n \leq k \log 2 < m + \log (n+1)$
kの満たすべき条件は
$\begin{align}
\frac{m + \log n}{\log 2} \leq k < \frac{m + \log (n+1)}{\log 2}
\end{align}$
$k$が入る区間の幅を$x_n$とすると
$\begin{align}
x_n &= \frac{m + \log (n+1)}{\log 2} – \frac{m + \log n}{\log 2}\\
&= \frac{\log (n+1) – \log n}{\log 2}
\end{align}$
■先頭の数字がnとなる確率を求める
ところで
$x_1 + x_2 + x_3 + \cdots + x_9$
$\begin{align}
&= \frac{\log 2 + (\log 3 – \log 2) + (\log 4 – \log 3) + \cdots + (\log 10 – \log 9)}{\log 2}\\
&= \frac{1}{\log 2}
\end{align}$
よって
先頭の数字がnとなる確率は
$\begin{align}
p_n &= \frac{x_n}{x_1 + x_2 + x_3 + \cdots + x_9}\\
&= \frac{\frac{\log (n+1) – \log n}{\log 2}}{\frac{1}{\log 2}}\\
&= \log (n+1) – \log n
\end{align}$