「データサイエンスとAIの初歩」コースの話題から
正規分布ではプラスマイナス3シグマ内にデータ全体の99.7%が含まれることが知られています。シグマは標準偏差のことです。
このレベルで製品を管理すると1000個に3個の割合で欠陥品が出るということになります。
実際に正規分布乱数(シグマは1)を使って1000回乱数を発生させ、マイナス3シグマより小さいものが何個くらいあるのか調べてみることができます。
Pythonコードは以下のようになります。1000個のデータを並べ替えて最初の5個を表示しています。
import numpy as np
R = np.random.randn(1000)
R.sort()
for i in range(5):
print(R[i])
片側だけを調べているので平均すると1.5個くらいが欠陥品となります。
これに対して、シックスシグマは100万個あたりの欠陥品を3.4個のレベルにしようとする経営品質の改革活動のことです。
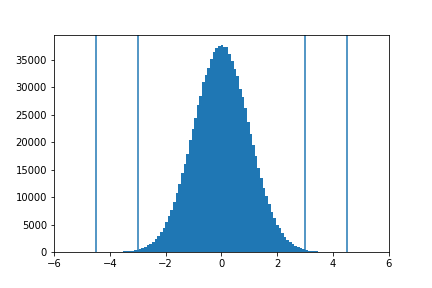
ここで注意が必要なのは正規分布でプラスマイナス6シグマをはみ出したのが欠陥品という意味ではないということです。平均値のゆらぎが一般に1.5シグマであることを考慮しなければならず、正規分布ではプラスマイナス4.5シグマで考える必要があります。
さらに100万個あたりで欠陥品が3.4個というのはプラスマイナスではなく片側だけのことを意味しています。
この場合も、正規分布乱数を使って100万回乱数を発生させ、4.5シグマより小さくなるのは何個あるのか確かめることができます。
Pythonコードは以下のようになります。
100万個の正規分布乱数データ(シグマは1)を発生し、4.5シグマより小さいデータの個数を数えています。
さらに10回繰り返して平均をとっています。
実際に計算してみるとマイナス4.5シグマより小さくなるのは確かに2個から4個くらいになることがわかります。
import numpy as np
n = 10
count = 0
for i in range(n):
R = np.random.randn(1000000)
count += sum(R < -4.5)
print('ave', count/n)
中高生の統計の学習にプログラムは最適なツールの一つです。