中高生向けEx-Gramプログラミング教室の上級コースではセルオートマトンの応用として感染症のシミュレーションを扱っています。以下にシミュレーション結果の一例をご紹介します。
注:新型コロナウイルス感染症のデータを一部使用していますが、新型コロナウイルス感染症のシミュレーションではありません。
感染症の拡散に関しては簡単な数理モデルがあります。
参考文献:https://costep.open-ed.hokudai.ac.jp/like_hokudai/contents/article/1792/
pの比率(vaccination rate)の人が手洗いを頻繁に行っていたり、予防接種を受けたりして感染を免れることができるものとします。感染を免れない人の割合は(1-p)となります。
(1-p)の割合の人の間でR₀(基本再生産数basic reproduction number)人の2次感染がおこるとすると、2次感染者数は(1-p)×R₀となります。この数値が1を下回ると大規模流行を防ぐことができるわけです。すなわちp>1-1/R₀が流行を防ぐ条件です。
例えばR₀=2.5(1人が2.5人にうつす)と仮定したとき、感染拡大を防ぐのに必要なpの値は0.6以上となります。60%の人が感染しないように努めていれば大流行を防ぐことができるというわけです。
以下ではR₀=2.5とし、pを0.1、0.2、0.3、0.4、0.5、0.6と変えながら、セルオートマトンによるシミュレーションを行いました。
その他の仮定として、
人口10万人の都市に縦横に人が整列しており人の移動はない、
ある時、都市の中央に1人の感染者が発生し、そこから感染が広がっていく、
感染後に一定期間を経ると回復する、
として時間発展を計算しました。
色で状態を表しており、
緑色はまだ感染していない人
赤色は感染した人
青色は感染したが一定期間後に回復した人
白はpの比率で決まる感染しない人
です。
■基本再生産数R₀=2.5、vaccination rate p=0.1の場合
ある時間が経過したときの様子は以下のようになります。感染が拡大しつつあります。中央部には回復した人たちがいます。
さらに時間が経過すると都市はほぼ全滅ですが、やがて回復します。
図の下の方のグラフは感染者数の推移を表しています。

■基本再生産数R₀=2.5、vaccination rate p=0.2の場合
感染拡大の速度は落ちますが、さらに時間が経過すると最終的には都市はほぼ全滅し、やがて回復します。

■基本再生産数R₀=2.5、vaccination rate p=0.3の場合
さらに感染拡大の速度は落ちますが、時間が経過すると最終的に都市はほぼ全滅し、やがて回復します。

■基本再生産数R₀=2.5、vaccination rate p=0.4の場合
感染拡大の速度はかなり落ちています。

さらに時間が経つと、以下のような状態となり、都市のかなりの部分が感染しますが、流行は止まります。

■基本再生産数R₀=2.5、vaccination rate p=0.5の場合
早い段階で拡散が食い止められています。これ以上進展することはありません。

■基本再生産数R₀=2.5、vaccination rate p=0.6の場合
簡単な数理モデルから得られる感染拡大防止に必要な条件です。
かなり初期の段階で拡散が食い止められています。これ以上進展することはありません。
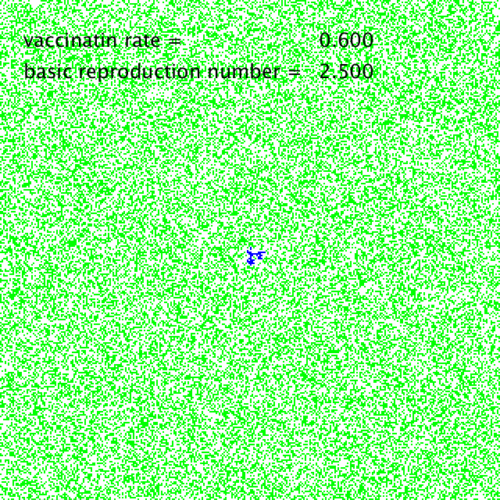
上記は簡易的なシミュレーションですが、一人一人が感染しないように努めることが重要であることがわかります。
さらに人の移動も考慮してみるとよいでしょう。